MMM Multidimensional Example Notebook#
In this notebook, we present an new experimental media mix model class to create multidimensional and customized marketing mix models. To showcase its capabilities, we extend the MMM Example Notebook simulation to create a multidimensional hierarchical model.
Warning
Even though the new MMM class is an experimental class, it is fully functional and can be used to create multidimensional marketing mix models. This model is under active development and will be further improved in the future (feedback welcome!).
Prepare Notebook#
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns
from pymc_marketing.mmm import GeometricAdstock, LogisticSaturation
from pymc_marketing.mmm.additive_effect import LinearTrendEffect
from pymc_marketing.mmm.linear_trend import LinearTrend
from pymc_marketing.mmm.multidimensional import MMM
from pymc_marketing.paths import data_dir
from pymc_marketing.prior import Prior
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = [12, 7]
plt.rcParams["figure.dpi"] = 100
plt.rcParams["xtick.labelsize"] = 10
plt.rcParams["ytick.labelsize"] = 8
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "retina"
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/multidimensional.py:59: FutureWarning: This functionality is experimental and subject to change. If you encounter any issues or have suggestions, please raise them at: https://github.com/pymc-labs/pymc-marketing/issues/new
warnings.warn(warning_msg, FutureWarning, stacklevel=1)
seed: int = sum(map(ord, "mmm_multidimensional"))
rng: np.random.Generator = np.random.default_rng(seed=seed)
Read Data#
We read the simulated data from the MMM Example Notebook.
data_path = data_dir / "mmm_example.csv"
raw_data_df = pd.read_csv(data_path, parse_dates=["date_week"])
raw_data_df = raw_data_df.rename(columns={"date_week": "date"})
raw_data_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 179 entries, 0 to 178
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 date 179 non-null datetime64[ns]
1 y 179 non-null float64
2 x1 179 non-null float64
3 x2 179 non-null float64
4 event_1 179 non-null float64
5 event_2 179 non-null float64
6 dayofyear 179 non-null int64
7 t 179 non-null int64
dtypes: datetime64[ns](1), float64(5), int64(2)
memory usage: 11.3 KB
To generate a multidimensional dataset, we simply duplicate and perturb the simulated target data with noise. We assign the different groups to different geography (geos) levels. We keep the same media variables for both geos.
# Create copies of the original data foo both geos
a_data_df = raw_data_df.copy().assign(geo="geo_a")
b_data_df = raw_data_df.copy().assign(geo="geo_b")
# Add noise to the target variable for the second geo
b_data_df["y"] = b_data_df["y"] + 500 * rng.normal(size=len(b_data_df))
# Concatenate the two datasets
data_df = pd.concat([a_data_df, b_data_df])
data_df.head()
| date | y | x1 | x2 | event_1 | event_2 | dayofyear | t | geo | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2018-04-02 | 3984.662237 | 0.318580 | 0.0 | 0.0 | 0.0 | 92 | 0 | geo_a |
| 1 | 2018-04-09 | 3762.871794 | 0.112388 | 0.0 | 0.0 | 0.0 | 99 | 1 | geo_a |
| 2 | 2018-04-16 | 4466.967388 | 0.292400 | 0.0 | 0.0 | 0.0 | 106 | 2 | geo_a |
| 3 | 2018-04-23 | 3864.219373 | 0.071399 | 0.0 | 0.0 | 0.0 | 113 | 3 | geo_a |
| 4 | 2018-04-30 | 4441.625278 | 0.386745 | 0.0 | 0.0 | 0.0 | 120 | 4 | geo_a |
Let’s plot the target variable for each geo to visually inspect the difference.
g = sns.relplot(
data=data_df,
x="date",
y="y",
color="black",
col="geo",
col_wrap=1,
kind="line",
height=4,
aspect=3,
)
/Users/juanitorduz/Documents/envs/pymc-marketing-env/lib/python3.12/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
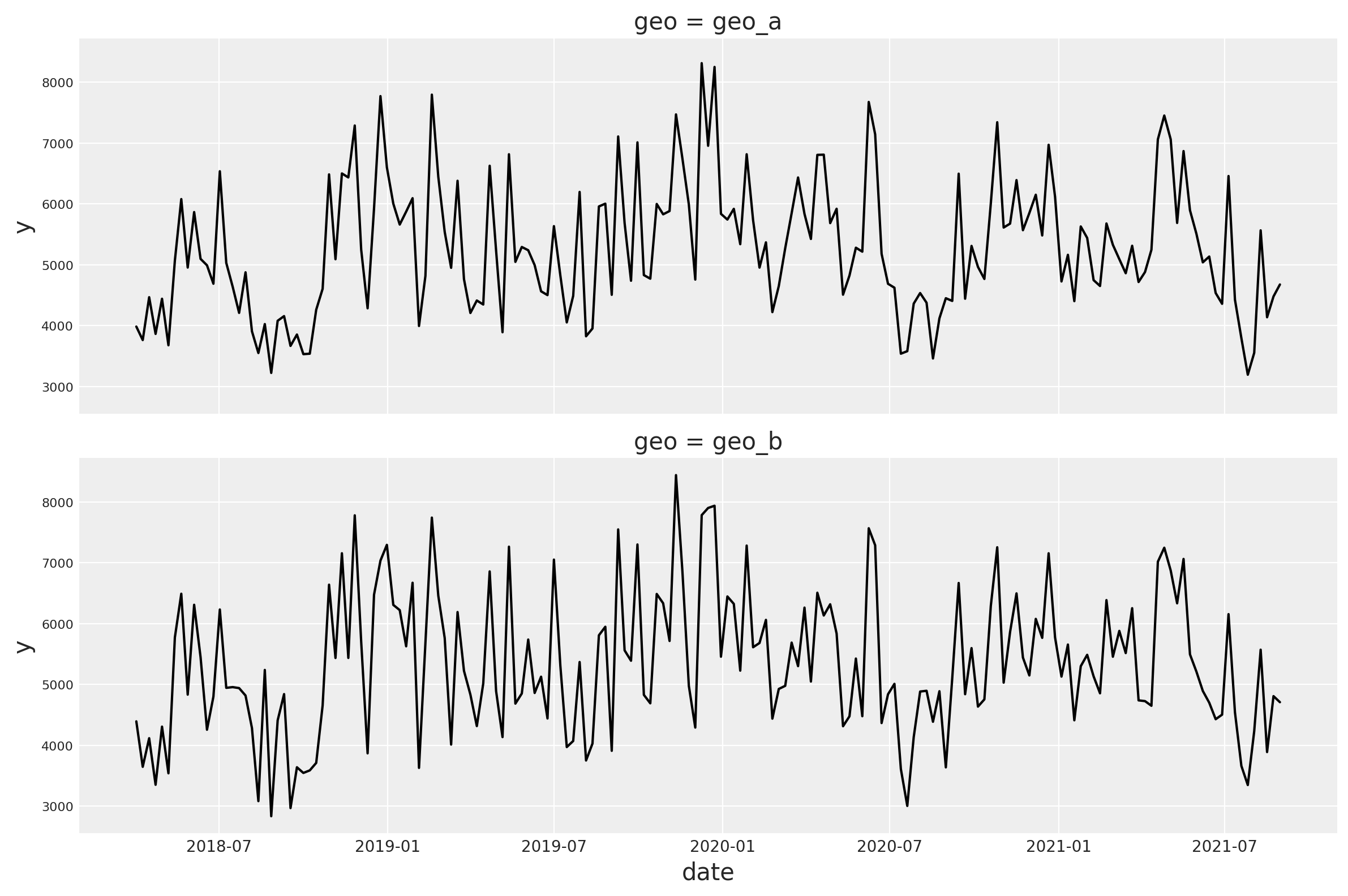
Overall, the targets follow a similar global pattern but the short term fluctuations are different.
Prior Specification#
Here is where we see the main power of the new class. We can now specify different priors for different geos and even build custom hierarchies.
Recall from the MMM Example Notebook that we wan to use the spend shares as a prior for the beta parameters in the saturation function. Let’s compute those shares across geos.
channel_columns = ["x1", "x2"]
n_channels = len(channel_columns)
sum_spend_geo_channel = data_df.groupby(["geo"]).agg({"x1": "sum", "x2": "sum"})
spend_share = (
sum_spend_geo_channel.to_numpy() / sum_spend_geo_channel.sum(axis=1).to_numpy()
)
prior_sigma = n_channels * spend_share
Now we are ready to specify the priors for the saturation function. For the beta parameters, we use a half-normal distribution with a sigma parameter that is computed as a function of the spend shares. For the lambda parameters, we add a hierarchical structure to the parameters of the gamma prior. This has the effect of sharing information across geos. If you need an introduction on Bayesian hierarchical models, check out the comprehensive example “A Primer on Bayesian Methods for Multilevel Modeling” in the PyMC documentation. Please note the dims argument in the priors is used to specify the dimensions of the distribution. Here you can control the dimensions along which the hierarchies are defined.
saturation = LogisticSaturation(
priors={
"beta": Prior("HalfNormal", sigma=prior_sigma, dims=("channel", "geo")),
"lam": Prior(
"Gamma",
mu=Prior("LogNormal", mu=np.log(3), sigma=np.log(1.5), dims="geo"),
sigma=Prior("LogNormal", mu=np.log(1), sigma=np.log(1.5), dims="geo"),
dims=("channel", "geo"),
),
}
)
saturation.model_config
{'saturation_lam': Prior("Gamma", mu=Prior("LogNormal", mu=1.0986122886681098, sigma=0.4054651081081644, dims="geo"), sigma=Prior("LogNormal", mu=0.0, sigma=0.4054651081081644, dims="geo"), dims=("channel", "geo")),
'saturation_beta': Prior("HalfNormal", sigma=[[1.31263903 0.68736097]
[1.31263903 0.68736097]], dims=("channel", "geo"))}
For the adstock parameters we do not add any hierarchical structure. We simply keep the same prior for all the geos.
adstock = GeometricAdstock(
priors={"alpha": Prior("Beta", alpha=2, beta=3, dims="channel")}, l_max=8
)
adstock.model_config
{'adstock_alpha': Prior("Beta", alpha=2, beta=3, dims="channel")}
We complete the model specification with similar priors as in the MMM Example Notebook. Please be aware on how to specify the priors dimensions.
model_config = {
"intercept": Prior("Normal", mu=0.5, sigma=0.5, dims="geo"),
"gamma_control": Prior("Normal", mu=0, sigma=0.5, dims="control"),
"gamma_fourier": Prior(
"Laplace", mu=0, b=Prior("HalfNormal", sigma=0.2), dims=("geo", "fourier_mode")
),
"likelihood": Prior(
"TruncatedNormal",
lower=0,
sigma=Prior("HalfNormal", sigma=Prior("HalfNormal", sigma=1.5)),
dims=("date", "geo"),
),
}
Model Definition#
We are now ready to define the model class. The API is very similar to the one in the MMM Example Notebook.
# Base MMM model specification
mmm = MMM(
date_column="date",
target_column="y",
channel_columns=["x1", "x2"],
control_columns=["event_1", "event_2"],
dims=("geo",),
scaling={
"channel": {"method": "max", "dims": ()},
"target": {"method": "max", "dims": ()},
},
adstock=adstock,
saturation=saturation,
yearly_seasonality=2,
model_config=model_config,
)
Tip
Observe we have the following two new arguments:
dims: a tuple of strings that specify the dimensions of the model.scaling: a dictionary that specifies the scaling method and dimensions for the target and media variables. In this case we leave the dimensions empty as we want to scale the target variable for each geo (see details below).
We can add additional components to the model mean component. Here, for example, we add a hierarchical linear trend component (with changepoints).
linear_trend = LinearTrend(
priors={
"delta": Prior(
"Laplace",
mu=0,
b=Prior("HalfNormal", sigma=0.2),
dims=("changepoint", "geo"),
),
},
n_changepoints=5,
include_intercept=False,
dims=("geo"),
)
linear_trend_effect = LinearTrendEffect(linear_trend, prefix="trend")
mmm.mu_effects.append(linear_trend_effect)
We can now prepare the training data.
x_train = data_df.drop(columns=["y"])
y_train = data_df["y"]
To build the model, we need to specify the training data and the target variables.
Tip
We do not need to build the model, we can simply fit the model. This is just to inspect the model structure.
mmm.build_model(X=x_train, y=y_train)
Let’s look into the model graph:
pm.model_to_graphviz(mmm.model)
It is great to see that the model automatically vectorizes and creates the expected hierarchies and dimensions 🚀!
As we are scaling our data internally, we can add deterministic terms to recover the component contributions in the original scale.
mmm.add_original_scale_contribution_variable(
var=[
"channel_contribution",
"control_contribution",
"intercept_contribution",
"yearly_seasonality_contribution",
]
)
pm.model_to_graphviz(mmm.model)
Coming back to the scalers, we can get them as an xarray dataset.
scalers = mmm.get_scales_as_xarray()
scalers
{'channel_scale': <xarray.DataArray '_channel' (geo: 2, channel: 2)> Size: 32B
array([[0.99665813, 0.99437431],
[0.99665813, 0.99437431]])
Coordinates:
* geo (geo) object 16B 'geo_a' 'geo_b'
* channel (channel) object 16B 'x1' 'x2',
'target_scale': <xarray.DataArray '_target' (geo: 2)> Size: 16B
array([8312.40754439, 8440.6617456 ])
Coordinates:
* geo (geo) object 16B 'geo_a' 'geo_b'}
As expected, from the model definition, we have scalers for the target and media variables across geos.
Prior Predictive Checks#
Before fitting the model, we can inspect the prior predictive distribution.
prior_predictive = mmm.sample_prior_predictive(X=x_train, y=y_train, samples=1_000)
Sampling: [adstock_alpha, delta, delta_b, gamma_control, gamma_fourier, gamma_fourier_b, intercept_contribution, saturation_beta, saturation_lam, saturation_lam_mu, saturation_lam_sigma, y, y_sigma, y_sigma_sigma]
g = sns.relplot(
data=data_df,
x="date",
y="y",
color="black",
col="geo",
col_wrap=1,
kind="line",
height=4,
aspect=3,
)
axes = g.axes.flatten()
for ax, geo in zip(axes, mmm.model.coords["geo"], strict=True):
az.plot_hdi(
x=mmm.model.coords["date"],
# We need to scale the prior predictive to the original scale to make it comparable to the data.
y=(
prior_predictive.sel(geo=geo)["y"].unstack().transpose(..., "date")
* scalers["target_scale"].sel(geo=geo).item()
),
smooth=False,
color="C0",
hdi_prob=0.94,
fill_kwargs={"alpha": 0.3, "label": "94% HDI"},
ax=ax,
)
az.plot_hdi(
x=mmm.model.coords["date"],
y=(
prior_predictive.sel(geo=geo)["y"].unstack().transpose(..., "date")
* scalers["target_scale"].sel(geo=geo).item()
),
smooth=False,
color="C0",
hdi_prob=0.5,
fill_kwargs={"alpha": 0.5, "label": "50% HDI"},
ax=ax,
)
ax.legend(loc="upper left")
g.figure.suptitle("Prior Predictive", fontsize=16, fontweight="bold", y=1.03);
/Users/juanitorduz/Documents/envs/pymc-marketing-env/lib/python3.12/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
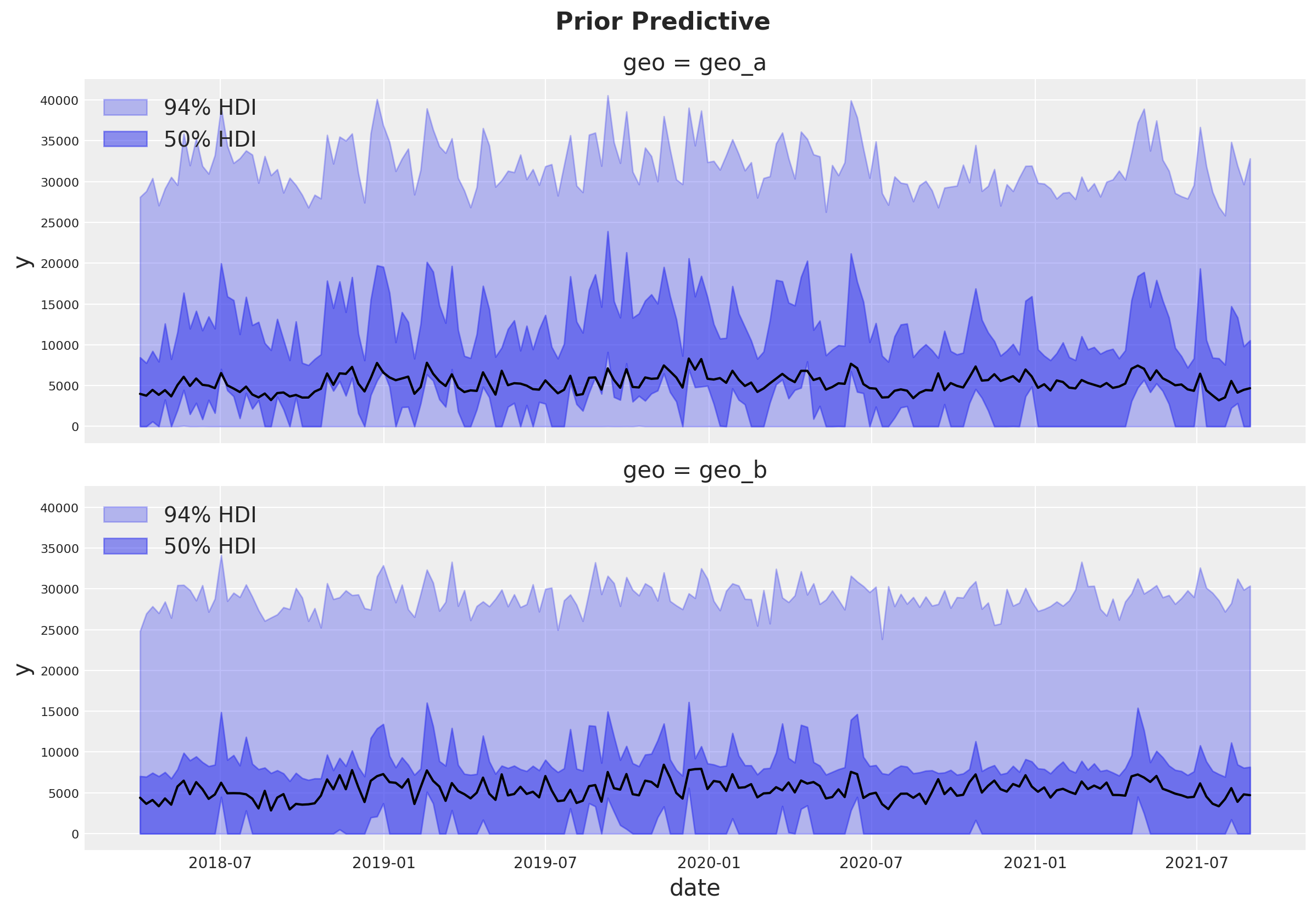
The prior predictive distribution looks good and not too restrictive.
Model Fitting#
We can now fit the model and generate the posterior predictive distribution.
mmm.fit(
X=x_train,
y=y_train,
chains=4,
target_accept=0.8,
nuts_sampler="nutpie",
random_seed=rng,
)
mmm.sample_posterior_predictive(
X=x_train,
extend_idata=True,
combined=True,
random_seed=rng,
)
Sampler Progress
Total Chains: 4
Active Chains: 0
Finished Chains: 4
Sampling for now
Estimated Time to Completion: now
| Progress | Draws | Divergences | Step Size | Gradients/Draw |
|---|---|---|---|---|
| 2000 | 0 | 0.16 | 63 | |
| 2000 | 0 | 0.16 | 63 | |
| 2000 | 0 | 0.17 | 31 | |
| 2000 | 0 | 0.15 | 63 |
Sampling: [y]
<xarray.Dataset> Size: 12MB
Dimensions: (date: 179, geo: 2, sample: 4000)
Coordinates:
* date (date) datetime64[ns] 1kB 2018-04-02 2018-04-09 ... 2021-08-30
* geo (geo) <U5 40B 'geo_a' 'geo_b'
* sample (sample) object 32kB MultiIndex
* chain (sample) int64 32kB 0 0 0 0 0 0 0 0 0 0 0 ... 3 3 3 3 3 3 3 3 3 3 3
* draw (sample) int64 32kB 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
Data variables:
y (date, geo, sample) float64 11MB 0.4822 0.4776 ... 0.5877 0.5815
Attributes:
created_at: 2025-03-25T16:51:22.870566+00:00
arviz_version: 0.20.0
inference_library: pymc
inference_library_version: 5.21.1The sampling looks good, no divergences and the r-hat values are close to \(1\).
mmm.idata.sample_stats.diverging.sum().item()

az.summary(
mmm.idata,
var_names=[
"adstock_alpha",
"delta",
"delta_b",
"gamma_control",
"gamma_fourier",
"intercept_contribution",
"saturation_beta",
"saturation_lam_sigma",
"saturation_lam",
"y_sigma_sigma",
"y_sigma",
],
)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| adstock_alpha[x1] | 0.399 | 0.033 | 0.338 | 0.459 | 0.001 | 0.000 | 2530.0 | 2961.0 | 1.00 |
| adstock_alpha[x2] | 0.160 | 0.037 | 0.092 | 0.226 | 0.001 | 0.001 | 2195.0 | 2975.0 | 1.00 |
| delta[0, geo_a] | 0.109 | 0.052 | 0.007 | 0.205 | 0.002 | 0.001 | 938.0 | 1217.0 | 1.01 |
| delta[0, geo_b] | 0.103 | 0.052 | 0.000 | 0.196 | 0.002 | 0.001 | 1167.0 | 1128.0 | 1.00 |
| delta[1, geo_a] | 0.020 | 0.067 | -0.114 | 0.152 | 0.002 | 0.002 | 926.0 | 1188.0 | 1.01 |
| delta[1, geo_b] | 0.012 | 0.068 | -0.130 | 0.138 | 0.002 | 0.002 | 1268.0 | 1305.0 | 1.01 |
| delta[2, geo_a] | -0.042 | 0.062 | -0.159 | 0.069 | 0.002 | 0.001 | 1766.0 | 1528.0 | 1.00 |
| delta[2, geo_b] | -0.030 | 0.060 | -0.156 | 0.075 | 0.001 | 0.001 | 2031.0 | 1667.0 | 1.00 |
| delta[3, geo_a] | 0.011 | 0.066 | -0.116 | 0.137 | 0.001 | 0.001 | 3373.0 | 2267.0 | 1.00 |
| delta[3, geo_b] | 0.030 | 0.073 | -0.083 | 0.197 | 0.001 | 0.001 | 3085.0 | 2013.0 | 1.00 |
| delta[4, geo_a] | 0.002 | 0.117 | -0.214 | 0.246 | 0.002 | 0.002 | 4703.0 | 2153.0 | 1.00 |
| delta[4, geo_b] | -0.002 | 0.146 | -0.276 | 0.252 | 0.003 | 0.004 | 3168.0 | 1551.0 | 1.01 |
| delta_b | 0.082 | 0.042 | 0.025 | 0.162 | 0.001 | 0.001 | 965.0 | 1758.0 | 1.01 |
| gamma_control[event_1] | 0.273 | 0.035 | 0.206 | 0.339 | 0.000 | 0.000 | 5945.0 | 2985.0 | 1.00 |
| gamma_control[event_2] | 0.325 | 0.035 | 0.258 | 0.391 | 0.000 | 0.000 | 5187.0 | 3024.0 | 1.00 |
| gamma_fourier[geo_a, sin_1] | 0.003 | 0.005 | -0.007 | 0.012 | 0.000 | 0.000 | 5751.0 | 3009.0 | 1.00 |
| gamma_fourier[geo_a, sin_2] | -0.056 | 0.005 | -0.066 | -0.046 | 0.000 | 0.000 | 5138.0 | 2790.0 | 1.00 |
| gamma_fourier[geo_a, cos_1] | 0.062 | 0.006 | 0.051 | 0.072 | 0.000 | 0.000 | 4715.0 | 2623.0 | 1.00 |
| gamma_fourier[geo_a, cos_2] | 0.002 | 0.005 | -0.008 | 0.011 | 0.000 | 0.000 | 4467.0 | 2673.0 | 1.00 |
| gamma_fourier[geo_b, sin_1] | 0.002 | 0.005 | -0.008 | 0.012 | 0.000 | 0.000 | 5285.0 | 2807.0 | 1.00 |
| gamma_fourier[geo_b, sin_2] | -0.044 | 0.006 | -0.054 | -0.033 | 0.000 | 0.000 | 5884.0 | 3219.0 | 1.00 |
| gamma_fourier[geo_b, cos_1] | 0.068 | 0.005 | 0.057 | 0.077 | 0.000 | 0.000 | 5389.0 | 2954.0 | 1.00 |
| gamma_fourier[geo_b, cos_2] | 0.001 | 0.005 | -0.009 | 0.010 | 0.000 | 0.000 | 4820.0 | 2858.0 | 1.00 |
| intercept_contribution[geo_a] | 0.355 | 0.020 | 0.318 | 0.395 | 0.001 | 0.000 | 1326.0 | 1842.0 | 1.00 |
| intercept_contribution[geo_b] | 0.351 | 0.020 | 0.314 | 0.388 | 0.001 | 0.000 | 1142.0 | 1713.0 | 1.00 |
| saturation_beta[x1, geo_a] | 0.368 | 0.032 | 0.314 | 0.428 | 0.001 | 0.001 | 1217.0 | 1106.0 | 1.00 |
| saturation_beta[x1, geo_b] | 0.388 | 0.043 | 0.332 | 0.446 | 0.001 | 0.001 | 1356.0 | 1735.0 | 1.00 |
| saturation_beta[x2, geo_a] | 0.243 | 0.066 | 0.185 | 0.322 | 0.003 | 0.002 | 1085.0 | 576.0 | 1.01 |
| saturation_beta[x2, geo_b] | 0.242 | 0.084 | 0.172 | 0.339 | 0.004 | 0.003 | 996.0 | 635.0 | 1.00 |
| saturation_lam_sigma[geo_a] | 0.987 | 0.383 | 0.341 | 1.655 | 0.007 | 0.005 | 3246.0 | 2945.0 | 1.00 |
| saturation_lam_sigma[geo_b] | 1.009 | 0.410 | 0.376 | 1.762 | 0.008 | 0.006 | 2819.0 | 2555.0 | 1.00 |
| saturation_lam[x1, geo_a] | 3.881 | 0.580 | 2.797 | 4.938 | 0.018 | 0.013 | 1068.0 | 1195.0 | 1.00 |
| saturation_lam[x1, geo_b] | 3.882 | 0.567 | 2.805 | 4.898 | 0.017 | 0.012 | 1229.0 | 1223.0 | 1.00 |
| saturation_lam[x2, geo_a] | 3.716 | 1.153 | 1.525 | 5.918 | 0.035 | 0.025 | 1032.0 | 556.0 | 1.01 |
| saturation_lam[x2, geo_b] | 3.143 | 0.980 | 1.371 | 5.095 | 0.032 | 0.022 | 936.0 | 604.0 | 1.00 |
| y_sigma_sigma | 0.508 | 0.610 | 0.015 | 1.676 | 0.009 | 0.007 | 5428.0 | 3428.0 | 1.00 |
| y_sigma | 0.049 | 0.002 | 0.045 | 0.052 | 0.000 | 0.000 | 6121.0 | 2949.0 | 1.00 |
_ = az.plot_trace(
data=mmm.fit_result,
var_names=[
"adstock_alpha",
"delta",
"delta_b",
"gamma_control",
"gamma_fourier",
"intercept_contribution",
"saturation_beta",
"saturation_lam_sigma",
"saturation_lam",
"total_media_contribution_original_scale",
"y_sigma_sigma",
"y_sigma",
],
compact=True,
backend_kwargs={"figsize": (15, 15), "layout": "constrained"},
)
plt.gcf().suptitle("Model Trace", fontsize=16, fontweight="bold", y=1.03);
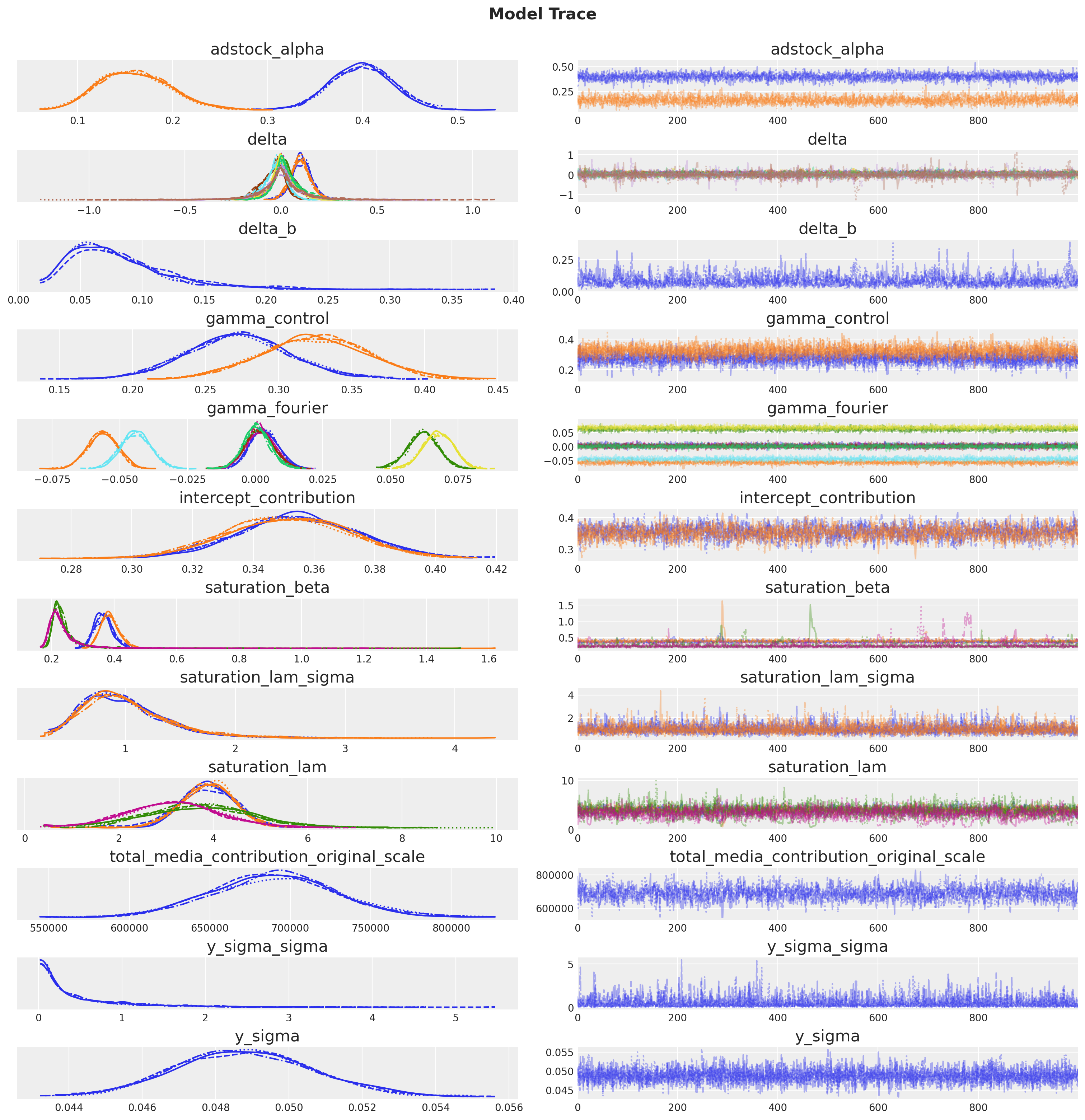
Posterior Predictive Checks#
We can now inspect the posterior predictive distribution. As before, we need to scale the posterior predictive to the original scale to make it comparable to the data.
fig, axes = plt.subplots(
nrows=len(mmm.model.coords["geo"]),
figsize=(12, 9),
sharex=True,
sharey=True,
layout="constrained",
)
for i, geo in enumerate(mmm.model.coords["geo"]):
ax = axes[i]
az.plot_hdi(
x=mmm.model.coords["date"],
y=(
mmm.idata["posterior_predictive"].sel(geo=geo)["y"]
* scalers["target_scale"].sel(geo=geo).item()
),
color="C0",
smooth=False,
hdi_prob=0.94,
fill_kwargs={"alpha": 0.2, "label": "94% HDI"},
ax=ax,
)
az.plot_hdi(
x=mmm.model.coords["date"],
y=(
mmm.idata["posterior_predictive"].sel(geo=geo)["y"]
* scalers["target_scale"].sel(geo=geo).item()
),
color="C0",
smooth=False,
hdi_prob=0.5,
fill_kwargs={"alpha": 0.4, "label": "50% HDI"},
ax=ax,
)
sns.lineplot(
data=data_df.query("geo == @geo"),
x="date",
y="y",
color="black",
ax=ax,
)
ax.legend(loc="upper left")
ax.set(title=f"{geo}")
fig.suptitle("Posterior Predictive", fontsize=16, fontweight="bold", y=1.03);
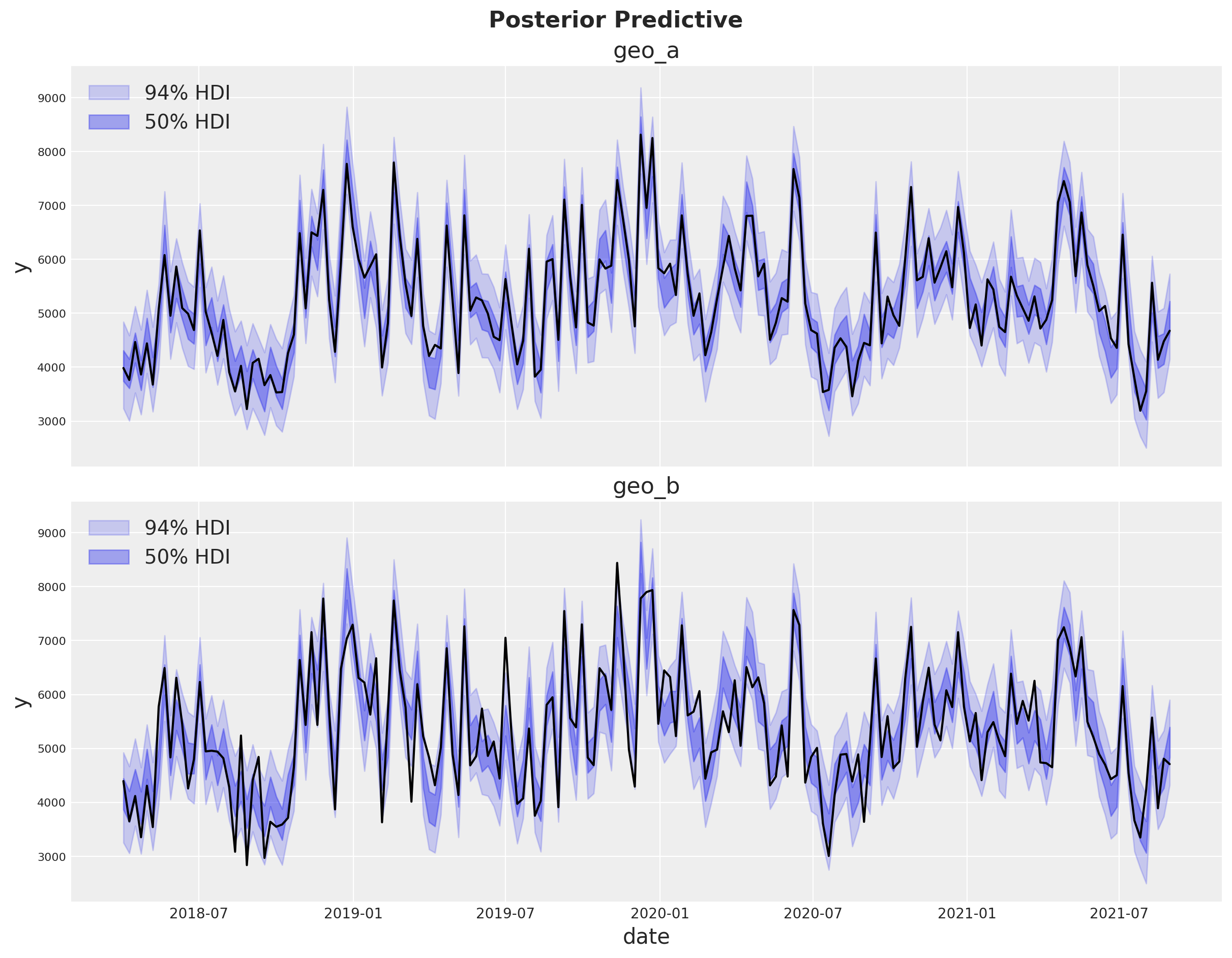
The fit looks very good!
Model Components#
We can extract the contributions of each component of the model in the original scale thanks to the deterministic variables added to the model.
fig, axes = plt.subplots(
nrows=len(mmm.model.coords["geo"]),
figsize=(15, 10),
sharex=True,
sharey=True,
layout="constrained",
)
for i, geo in enumerate(mmm.model.coords["geo"]):
ax = axes[i]
for j, channel in enumerate(mmm.model.coords["channel"]):
az.plot_hdi(
x=mmm.model.coords["date"],
y=mmm.idata["posterior"]["channel_contribution_original_scale"].sel(
geo=geo, channel=channel
),
color=f"C{j}",
smooth=False,
hdi_prob=0.94,
fill_kwargs={"alpha": 0.5, "label": f"94% HDI ({channel})"},
ax=ax,
)
az.plot_hdi(
x=mmm.model.coords["date"],
y=mmm.idata["posterior"]["intercept_contribution_original_scale"]
.sel(geo=geo)
.expand_dims({"date": mmm.model.coords["date"]})
.transpose(..., "date"),
color="C2",
smooth=False,
hdi_prob=0.94,
fill_kwargs={"alpha": 0.5, "label": "94% HDI intercept"},
ax=ax,
)
az.plot_hdi(
x=mmm.model.coords["date"],
y=mmm.idata["posterior"]["yearly_seasonality_contribution_original_scale"].sel(
geo=geo,
),
color="C3",
smooth=False,
hdi_prob=0.94,
fill_kwargs={"alpha": 0.5, "label": "94% HDI Fourier"},
ax=ax,
)
az.plot_hdi(
x=mmm.model.coords["date"],
y=mmm.idata["posterior"]["trend_effect"].sel(
geo=geo,
)
* mmm.scalers["_target"].sel(geo=geo).item(),
color="C4",
smooth=False,
hdi_prob=0.94,
fill_kwargs={"alpha": 0.5, "label": "94% HDI Trend"},
ax=ax,
)
for k, control in enumerate(mmm.model.coords["control"]):
az.plot_hdi(
x=mmm.model.coords["date"],
y=mmm.idata["posterior"]["control_contribution_original_scale"].sel(
geo=geo, control=control
),
color=f"C{5 + k}",
smooth=False,
hdi_prob=0.94,
fill_kwargs={"alpha": 0.5, "label": f"94% HDI control ({control})"},
ax=ax,
)
sns.lineplot(
data=data_df.query("geo == @geo"),
x="date",
y="y",
color="black",
label="y",
ax=ax,
)
ax.legend(
loc="upper center",
bbox_to_anchor=(0.5, -0.1),
ncol=4,
)
ax.set(title=f"{geo}")
fig.suptitle(
"Posterior Predictive - Channel Contributions",
fontsize=16,
fontweight="bold",
y=1.03,
);
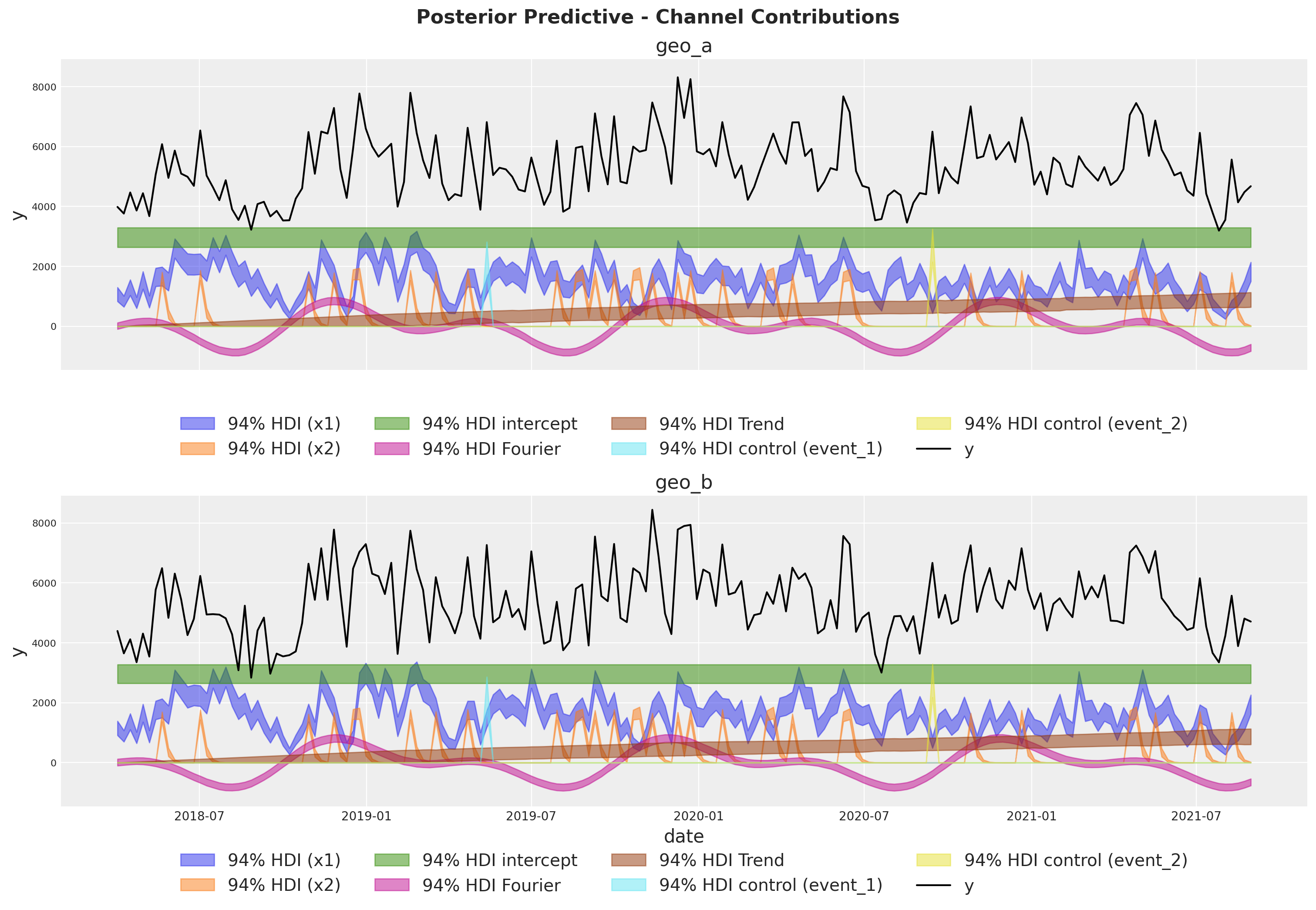
Media Deep Dive#
Next, we can look into the individual channel contributions across geos.
fig, axes = plt.subplots(
nrows=len(mmm.model.coords["geo"]),
ncols=len(mmm.model.coords["channel"]),
figsize=(12, 9),
layout="constrained",
)
for i, geo in enumerate(mmm.model.coords["geo"]):
for j, channel in enumerate(mmm.model.coords["channel"]):
ax = axes[i, j]
az.plot_hdi(
x=mmm.model.coords["date"],
y=mmm.idata["posterior"]["channel_contribution_original_scale"].sel(
geo=geo, channel=channel
),
color=f"C{j}",
smooth=False,
hdi_prob=0.94,
ax=ax,
)
ax.set_title(f"{geo} - {channel}")
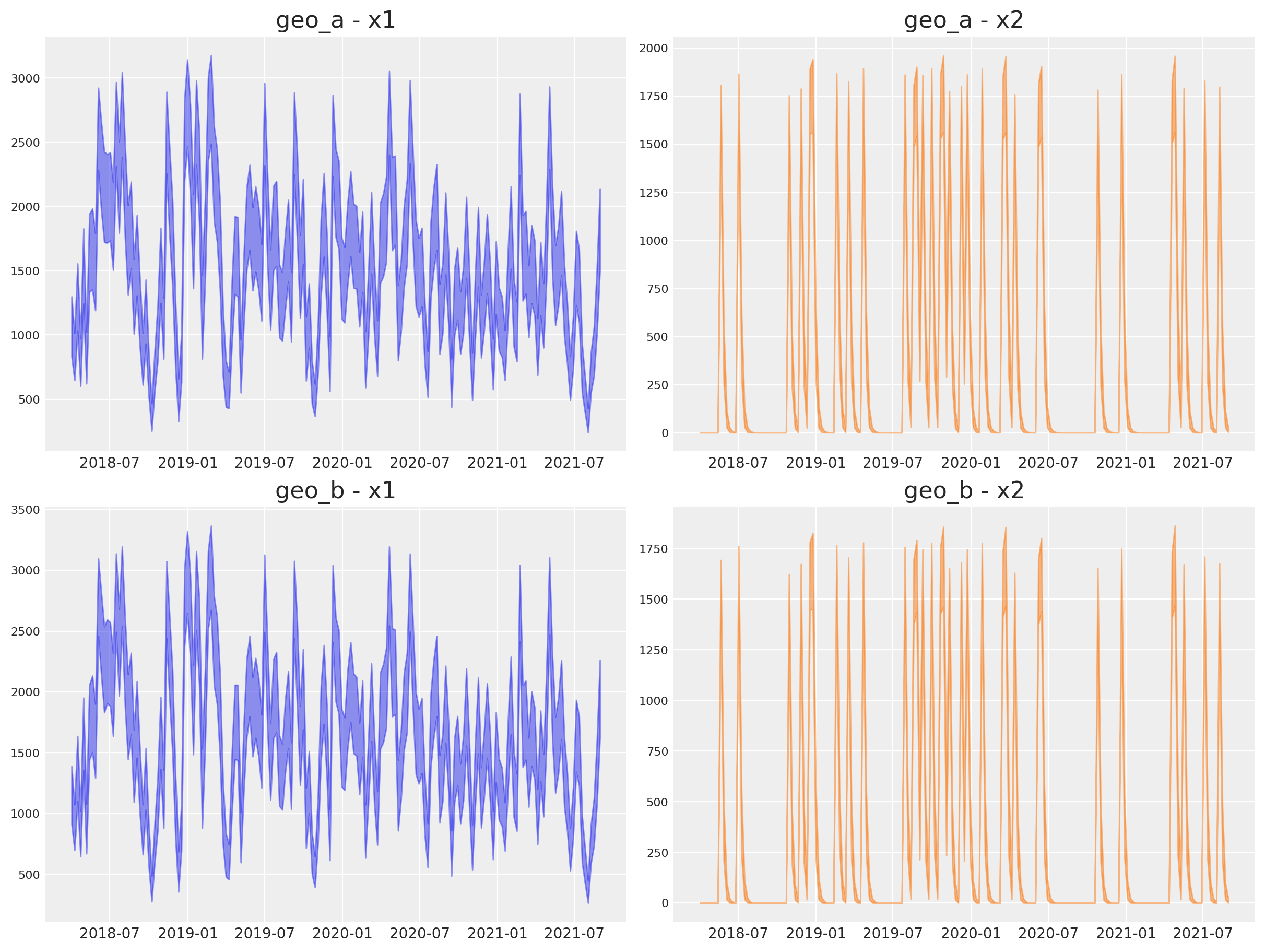
Observe that all the vectorization and heavy lifting is done under the hood by the new class.
This new class has a new plot name space that contains many plotting methods. For example, we can reproduce the plots above by simply calling:
fig, axes = mmm.plot.contributions_over_time(
var=["channel_contribution_original_scale"]
)
axes = axes.flatten()
for ax in axes:
ax.legend().remove()
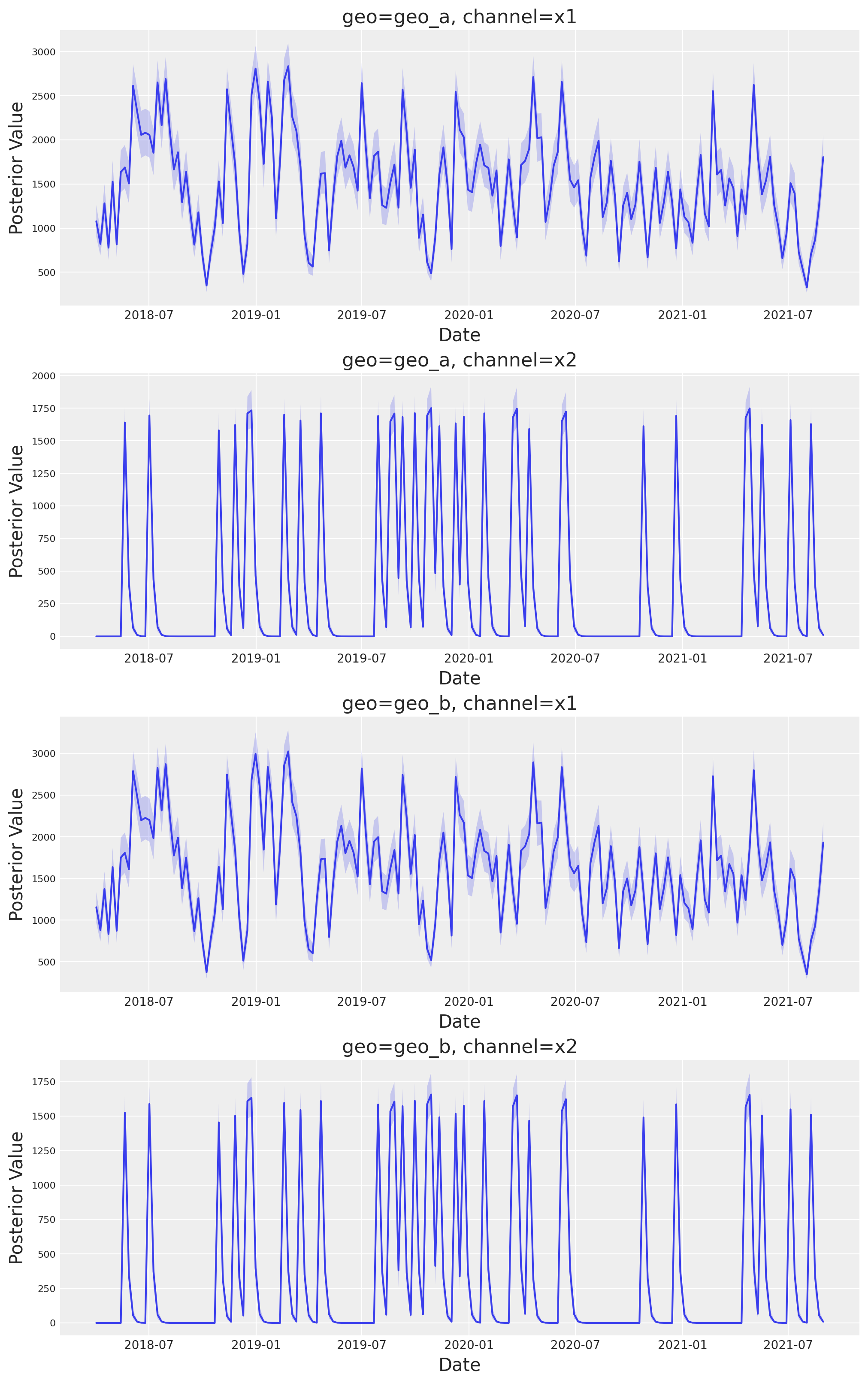
We can also plot the saturation curves for each channel and geo.
mmm.plot.saturation_curves_scatter(
width_per_col=8, height_per_row=4, original_scale=True
);
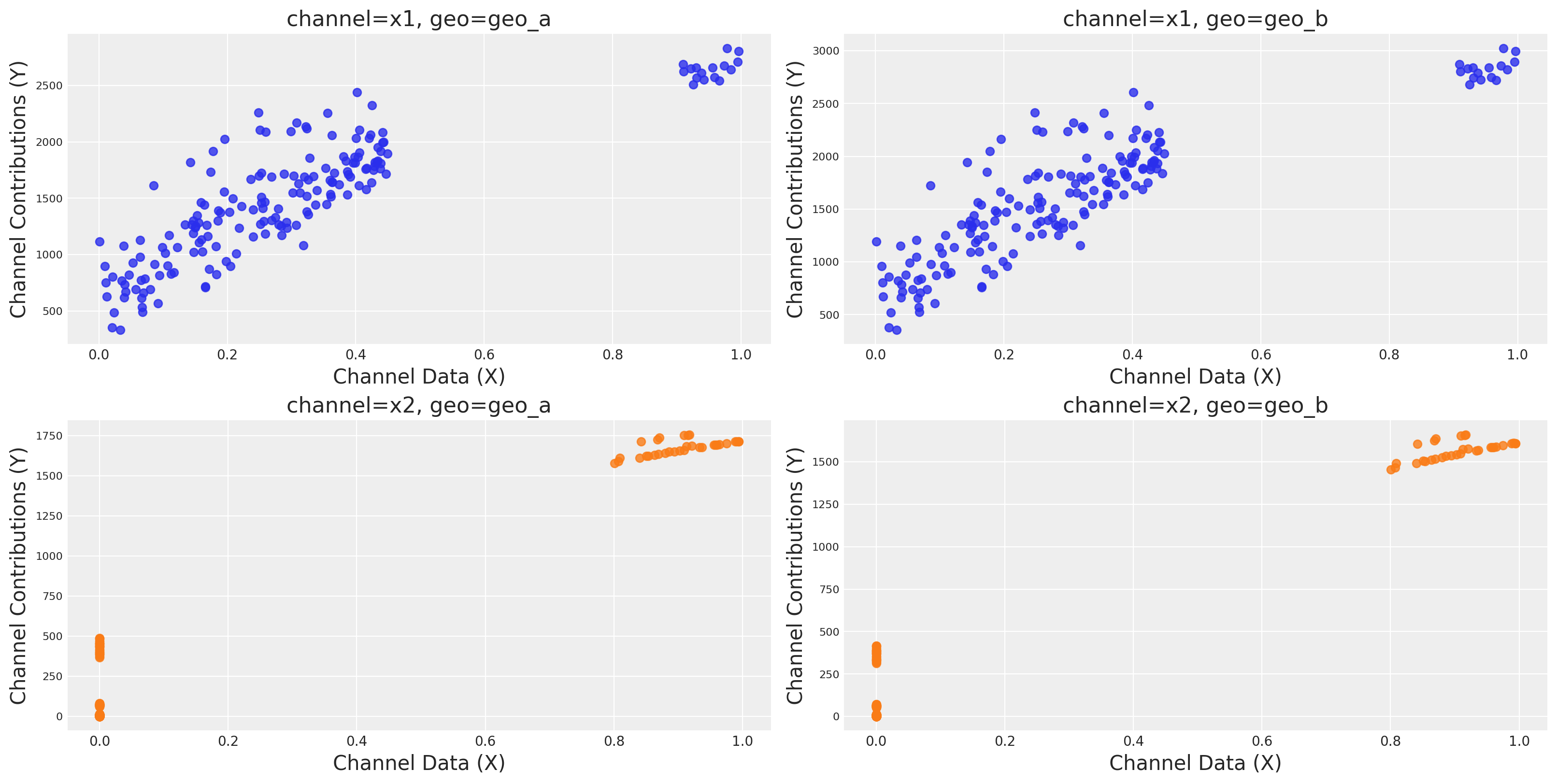
Out of Sample Predictions#
It is very important to be able to make predictions out of the sample. This is key for model validation, forward looking scenario planning and business decision making. Similarly as in the MMM Example Notebook, we assume the future spends are the same as the last day in the training sample. This way we can create a new dataset with the future dates and channel spends and use the model to make predictions.
last_date = x_train["date"].max()
# New dates starting from last in dataset
n_new = 7
new_dates = pd.date_range(start=last_date, periods=1 + n_new, freq="W-MON")[1:]
x_out_of_sample_geo_a = pd.DataFrame({"date": new_dates, "geo": "geo_a"})
x_out_of_sample_geo_b = pd.DataFrame({"date": new_dates, "geo": "geo_b"})
# Same channel spends as last day
x_out_of_sample_geo_a["x1"] = x_train.query("geo == 'geo_a'")["x1"].iloc[-1]
x_out_of_sample_geo_a["x2"] = x_train.query("geo == 'geo_a'")["x2"].iloc[-1]
x_out_of_sample_geo_b["x1"] = x_train.query("geo == 'geo_b'")["x1"].iloc[-1]
x_out_of_sample_geo_b["x2"] = x_train.query("geo == 'geo_b'")["x2"].iloc[-1]
# Other features
## Event 1
x_out_of_sample_geo_a["event_1"] = 0.0
x_out_of_sample_geo_a["event_2"] = 0.0
## Event 2
x_out_of_sample_geo_b["event_1"] = 0.0
x_out_of_sample_geo_b["event_2"] = 0.0
x_out_of_sample = pd.concat([x_out_of_sample_geo_a, x_out_of_sample_geo_b])
# Final dataset to generate out of sample predictions.
x_out_of_sample
| date | geo | x1 | x2 | event_1 | event_2 | |
|---|---|---|---|---|---|---|
| 0 | 2021-09-06 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 1 | 2021-09-13 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 2 | 2021-09-20 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 3 | 2021-09-27 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 4 | 2021-10-04 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 5 | 2021-10-11 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 6 | 2021-10-18 | geo_a | 0.438857 | 0.0 | 0.0 | 0.0 |
| 0 | 2021-09-06 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
| 1 | 2021-09-13 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
| 2 | 2021-09-20 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
| 3 | 2021-09-27 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
| 4 | 2021-10-04 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
| 5 | 2021-10-11 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
| 6 | 2021-10-18 | geo_b | 0.438857 | 0.0 | 0.0 | 0.0 |
Using the same sample_posterior_predictive method, we can now generate the forecast.
y_out_of_sample = mmm.sample_posterior_predictive(
x_out_of_sample,
extend_idata=False,
include_last_observations=True,
random_seed=rng,
)
y_out_of_sample
Sampling: [y]
<xarray.Dataset> Size: 544kB
Dimensions: (date: 7, geo: 2, sample: 4000)
Coordinates:
* date (date) datetime64[ns] 56B 2021-09-06 2021-09-13 ... 2021-10-18
* geo (geo) <U5 40B 'geo_a' 'geo_b'
* sample (sample) object 32kB MultiIndex
* chain (sample) int64 32kB 0 0 0 0 0 0 0 0 0 0 0 ... 3 3 3 3 3 3 3 3 3 3 3
* draw (sample) int64 32kB 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
Data variables:
y (date, geo, sample) float64 448kB 0.6105 0.6279 ... 0.7309 0.6514
Attributes:
created_at: 2025-03-25T16:51:30.255899+00:00
arviz_version: 0.20.0
inference_library: pymc
inference_library_version: 5.21.1fig, axes = plt.subplots(
nrows=2,
ncols=1,
figsize=(12, 10),
sharex=True,
sharey=True,
layout="constrained",
)
n_train_to_plot = 30
for ax, geo in zip(axes, mmm.model.coords["geo"], strict=True):
for hdi_prob in [0.94, 0.5]:
az.plot_hdi(
x=mmm.model.coords["date"][-n_train_to_plot:],
y=(
mmm.idata["posterior_predictive"].sel(geo=geo)["y"][
:, :, -n_train_to_plot:
]
* mmm.scalers["_target"].sel(geo=geo).item()
),
color="C0",
smooth=False,
hdi_prob=hdi_prob,
fill_kwargs={"alpha": 0.4, "label": f"{hdi_prob: 0.0%} HDI"},
ax=ax,
)
az.plot_hdi(
x_out_of_sample.query("geo == @geo")["date"],
(
y_out_of_sample["y"].sel(geo=geo).unstack().transpose(..., "date")
* mmm.scalers["_target"].sel(geo=geo).item()
),
color="C1",
smooth=False,
hdi_prob=hdi_prob,
fill_kwargs={"alpha": 0.4, "label": f"{hdi_prob: 0.0%} HDI"},
ax=ax,
)
ax.plot(
x_out_of_sample.query("geo == @geo")["date"],
y_out_of_sample["y"].sel(geo=geo).mean(dim="sample")
* mmm.scalers["_target"].sel(geo=geo).item(),
marker="o",
color="C1",
label="posterior predictive mean",
)
sns.lineplot(
data=data_df.query("(geo == @geo)").tail(n_train_to_plot),
x="date",
y="y",
marker="o",
color="black",
label="observed",
ax=ax,
)
ax.axvline(x=last_date, color="gray", linestyle="--", label="last observation")
ax.legend(
loc="upper center",
bbox_to_anchor=(0.5, -0.15),
ncol=3,
)
ax.set(title=f"{geo}")
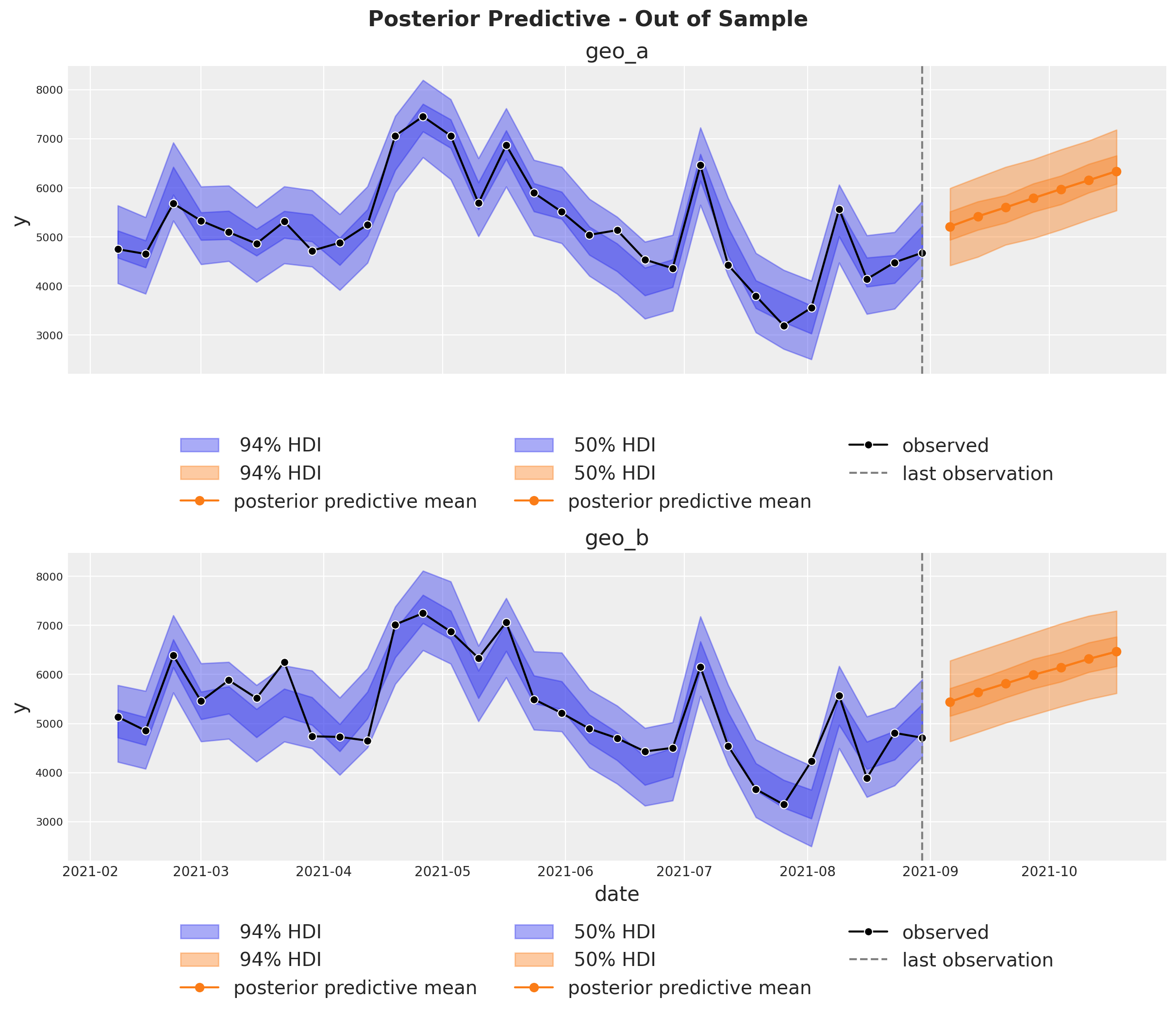
fig.suptitle(
"Posterior Predictive - Out of Sample", fontsize=16, fontweight="bold", y=1.03
);
Note
We are very excited about this new feature and the possibilities it opens up. We are looking forward to hearing your feedback!
%load_ext watermark
%watermark -n -u -v -iv -w -p pymc_marketing,pytensor,nutpie
Last updated: Tue Mar 25 2025
Python implementation: CPython
Python version : 3.12.9
IPython version : 8.32.0
pymc_marketing: 0.12.1
pytensor : 2.28.3
nutpie : 0.14.2
arviz : 0.20.0
pandas : 2.2.3
pymc : 5.21.1
pymc_marketing: 0.12.1
matplotlib : 3.10.0
numpy : 1.26.4
seaborn : 0.13.2
Watermark: 2.5.0
